index předchozí 1 2 3 4 5 6 7 následující

Cvičení sedmé

Přechodové systémy BPA a BPP. Konstrukce tabel pro BPP

1)Otázky:

Je daný proces posaný determ. konečným automatem. Jak zjistím, které stavy jsou bisimulačně ekvivalentní?
Najděte postačující podmínku na to, aby pro normovaný přechodový systém, byla jazyková ekvivalence shodná s bisimulací.
Pro normované BPA ověřte: ABC vlnka DBC => A vlnka D
Najděte nutnou podmínku, aby pro BPA platilo AA vlnka A.

2)Dána BPA algebra. Najděte přechodový systém, který je určen

 X -a-> XBB
 X -c-> epsilon
 B -a-> BBB
 B -b-> epsilon

3) Jaký jazyk generuje následující BPA?

 X -a-> XA
 X -b-> XB
 X -c-> epsilon
 A -a-> epsilon
 B -b-> epsilon

4) Nakreslete přechodový systém určený BPP algebrou

 X -a-> X|B
 X -c-> X|D
 B -b-> epsilon
 D -d-> epsilon
(X -e-> epsilon)

5) Vyjádřete daný přechodový systém BPA i BPP syntaxí:

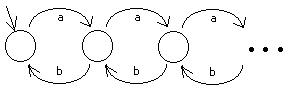
6) BPA syntaxí:

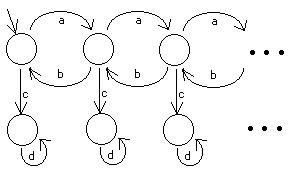
7) BPP syntaxí:

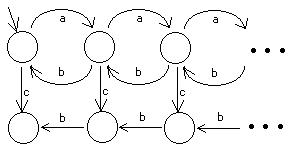
8) BPA syntaxí:

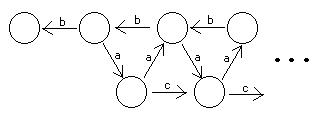
9) BPP syntaxí:

10) Zkonstruujte BPP tablo X1=X2

 X1 = a(X2|X3) + b
 X2 = aX4 + b
 X3 = cX1
 X4 = a(X3|X4) + c(X1|X1) + bX3

11) Zkonstruujte BPP tablo X1=X2

 X1 = a(X1|X4)
 X2 = a(X2|X3)
 X3 = a(X2|X3²) + b
 X4 = b