index předchozí 1 2 3 4 5 6 7 následující

Cvičení páté

LR(k), LALR(k) analyzátory, bisimulace

1) Rozhodněte, zda gramatika LR(0), SLR(1), LALR(1), LR(1)

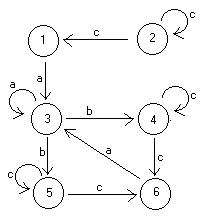
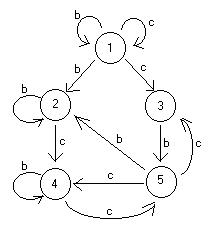
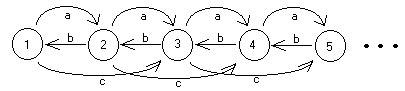
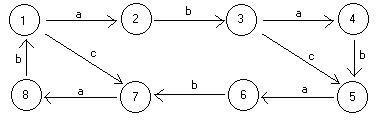
 S'-> S
 S -> aAd
 S -> bBd
 S -> aBc
 S -> bAc
 A -> c 
 B -> c

 S' -> S
 S -> AB
 A -> a
 B -> CD
 B -> aE
 C -> ab
 D -> bb
 E -> bba

2) Zkonstruujte LALR(1) analyzátor

 S'-> S
 S -> aAb
 S -> c
 S -> cB
 A -> bS
 A -> Bc
 B -> c

3) Zkonstruujte iniciální stav LR(2) automatu

 R'-> R
 R -> RR
 R -> R+R
 R -> (R)
 R -> a

4) Proveďte LR(1) analýzu

 S'-> S
 S -> aAS
 S -> epsilon
 A -> bb

5) Konstruujte analyzátory a analyzujte slova

 S -> AB
 A -> 0A1
 A -> epsilon
 B -> 1B
 B -> 1

 S -> aAd
 S -> bAc
 S -> aBc
 S -> bBd
 A -> xA
 A -> x
 B -> xB
 B -> x

 S -> ASB
 S -> ASC
 A -> a
 B -> ba
 C -> ca

 S'-> S
 S -> CBa
 S -> bBS
 B -> b
 C -> a
 C -> epsilon

 S'-> S
 S -> aAS
 S -> epsilon
 A -> bb

 S'-> S
 S -> SaA
 S -> c
 A -> Bb
 A -> epsilon
 B -> epsilon

 S'-> S
 S -> ddX
 X -> aX
 X -> epsilon

6) Pro daný přechodový systém najděte všechny dvojice bisimulačně ekvivalentních stavů metodou hry. Pomocí bisimulačního kolapsu k němu zkonstruujte ekvivalentní přechodový systém.

7) Pro daný přechodový sytém najděte maximálníá bisimulaci metodou postupných aproximací.

8) Je dán přechodový systém P₁ (nekonečně stavový). Zkonstruujte přechodový systém P₂ takový, aby platilo:

P₂ má stav I takový, že I vlnka 1
P₂ je konečně stavový

Jaká je maximální bisimulace pro P₁?
P1:

9) Najděte konečné automaty A₁,A₂ takové, aby

L(A₁) = L(A₂)
L(A₁) je nekonečný
Počáteční stavy automatů A₁, A₂ nejsou bisimulačně ekvivalentní

10) Dokažte nebo vyvraťte: 2 je bisimuláčně ekvivalentní 8; Najděte maximální bisimulaci.

11) Najděte nejmenší n, takové aby platilo 3 není ve vlnka_n s 4, ale 3 je ve vlnka_n-1 s 4.
Najděte maximální bisimulaci. Faktorizujte podle relace bisimulace.