i3dlib

Documentation

i3d::ImplicitLODScheme

i3d::ImplicitLODScheme< VOXELIN, VOXELOUT > Class Template Reference

This class is root abstract class for filters, which can be computed by simple LOD numerical scheme. This class implements the skeleton of numerical semi-implicit LOD (locally one dimensional) scheme. Instances of this class will not produce any usable output. To obtain fully functional filter try to instantiate some offspring of this class. As an example can serve the LODGaussianBlur class. More...

#include <LevelSet.h>

Inheritance diagram for i3d::ImplicitLODScheme< VOXELIN, VOXELOUT >:

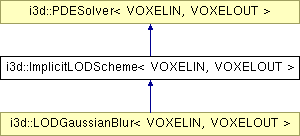
i3d::PDESolver< VOXELIN, VOXELOUT > i3d::LODGaussianBlur< VOXELIN, VOXELOUT > List of all members.

Public Member Functions

virtual void ComputeChange ()

Protected Attributes

valarray< VOXELOUT > Diag
 The coefficients of the main diagonal are saved in this valraay.
valarray< VOXELOUT > SDiag
 The coefficients of the supper diagonal are saved in this valraay.
valarray< VOXELOUT > PDiag
 Temporal variable.
valarray< VOXELOUT > PSDiag
 Temporal variable.

Detailed Description

template<class VOXELIN, class VOXELOUT>
class i3d::ImplicitLODScheme< VOXELIN, VOXELOUT >

This class is root abstract class for filters, which can be computed by simple LOD numerical scheme. This class implements the skeleton of numerical semi-implicit LOD (locally one dimensional) scheme. Instances of this class will not produce any usable output. To obtain fully functional filter try to instantiate some offspring of this class. As an example can serve the LODGaussianBlur class.

There are some linear filters (i.e. Gaussian blur) which have following features:

This abstract class implements the skeleton of numerical semi-implicit LOD (locally one dimensional) scheme. There is no sister function class like for the (ExplicitScheme,ExplicitSchemeFunction) and (PDESolver, PDESolverFunction) pairs. All the functionality of the implicit numerical scheme is implemented in this class. The LOD scheme is absolute stable fo all time steps, there is no limitation to the size of time step $ \tau $. 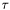The main advantage of solving linear filters with LOD scheme is the constant amount of time which they need to convolve the image with convolution kernel of arbitrary size. The offsprings of this abstract class modificate the input image by solving following partial differential equation:

\[ u_t = F(u), \]

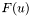where $ F(u) $ is some linear function of spatial derivatives of u.

The discretisation of the equation is usually written in the vector matrix form:

\[ \prod \limits_{l=1}^{m} (I - \tau A_l(u^{n})) u^{n+1} = u^{n} , \]

where m is the number of dimensions, 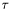$\tau$ is the time step. Solving of one forward iteration of this equation leads to finding the solution of the linear system of equations.

The LOD scheme solves this equation dimension by dimension by taking solutions of the folowing equation in particular direction (x,y) as input for finding soluton in following direction (y,z).

\[ u^{n+1} = (I - \tau A(u^n))^{-1} u^n \]

The solution of above equation in each direction leads to solving the linear system of equations in one iteration step. If we order the voxels extra for each direction, the matrix A becomes threediagonal and there exist fast methods for finding solutions of such matrices. This class uses LAPACK routines to find solutions of three diagonal linear system. The i3d library must be linked with lapack library to obtain fully functionality of this class.

The implementation of this class is based on the article
Joachim Weickert, Bart M. ter Haar Romeny, Max A. Viergever, Efficient and Reliable Schemes for Nonlinear Diffusion Filtering , IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 6, NO. 3, PP. 398-410, MARCH 1998.

The typical code for using the linear filters, which are offsprings of this class, is shown bellow. The example code uses the LOD implementation of Gaussian Blur filter (class LODGaussianBlur). 

    .....
   
   Image3d<GRAY8> i;
   Image3d<float> fimg;
   i.ReadImage('input.tif'); // read input image
   LODGaussianBlur<GRAY8,float> G(i,fimg);
   G.SetSigma(4.0);
   G.SetMaximumNumberOfIterations(1);
   G.SetSpacing(1.0,1.0,3.0); // optional if we want to set spacing different from the default settings.
   G.Execute();
   
   ......
Author:
Jan Hubený xhubeny@fi.muni.cz
Date:
2005

Member Function Documentation

template<class VOXELIN, class VOXELOUT>
void i3d::ImplicitLODScheme< VOXELIN, VOXELOUT >::ComputeChange (  )  [virtual]

One iteration of the LOD scheme will be performed after calling this method.

Reimplemented from i3d::PDESolver< VOXELIN, VOXELOUT >.

The documentation for this class was generated from the following files:

Generated by doxygen