index předchozí 1 2 3 4 5 6 7 8 9 10 11 12 následující

Cvičení třetí

Minimalizace KA, nedeterministické KA, (M-)Nerodova věta

1) Odstraňte nedosažitelné stavy z KA zadaného tabulkou a převeďte do kanonického tvaru:

stav pod a pod b

=> 1 5 2

2 2 8

3 2 7

<= 4 9 4

5 2 1

6 2 5

<= 7 8 6

8 2 4

9 8 9

{Řešení: Nepoužitelné stavy: 3,6 a 7}

Ověřte zda je výsledný automat ekvivalentní s tímto automatem:

stav pod a pod b

=> 1 4 2

2 2 5

3 3 6

4 4 2

<= 5 5 3

<= 6 6 2

stav pod a pod b

1 3 1

=> 2 9 4

3 5 1

<= 4 9 4

5 8 5

6 5 4

<= 7 6 9

8 10 10

9 7 9

10 8 1

Ověřte zda je výsledný automat ekvivalentní s tímto automatem:

stav pod a pod b

A B A

<= B C A

C D E

D D D

=>E A E

2) Pro následující KA zadané tabulkou:

Oveřte, že všechny stavy jsou dosažitelné
Zkonstruujte minimální automat
Minimální automat zapište v kanonickém tvaru

stav pod a pod b

=> 1 2 3

2 5 2

3 3 5

<= 4 12 2

<= 5 7 8

6 4 9

7 12 11

8 4 6

9 10 8

<= 10 3 2

<= 11 12 6

12 3 10

stav pod a pod b

<=> 1 3 2

2 6 4

3 3 5

<= 4 4 2

5 10 8

6 6 7

<= 7 7 5

<= 8 8 2

<= 9 11 2

10 10 9

<= 11 11 5

3) Ověřte, zda KA z příkladu 2 je ekvivalentní s následujícím KA zadaným tabulkou

stav pod a pod b

A A C

=> B D A

<= C D A

D C D

4) Navrhněte nedet. KA pro následující jazyky:

L={ w náleží {a,b,c,d}^* | w obsahuje podslovo abbc nebo bba nebo aba}
L={ w náleží {a,b,c}^* | w obsahuje podslovo abbc nebo acbca nebo bcabb}
L={ w náleží {a,b,c,d}^* | w končí řetězcem aaaa}
L={ w náleží {0,1}^* | w má čtvrtý symbol od konce 1}
L={ w náleží {0,1}^* | w končí řetězcem 0101 1}
L=(0^*1 sjednoceno (0⁺1^*0)^*)^*
L=(000^* + 111^*)^*

5) K daným nedet. KA zkonstrujte det. KA

stav pod a pod b pod c

=> 1 {2,3} {3,4} {1}

<= 2 {3} {4} {2}

3 {1,2,3} {1} {3,4}

4 {1} {1} {3,4}

stav pod a pod b pod c

=> 1 {1,2} {1} {1}

<= 2 {} {3} {}

3 {} {} {4}

4 {5} {} {}

5 {} {6} {}

6 {7} {} {}

<= 7 {} {} {}

6) Popište jazyk akceptovaný automatem: (DÚ)

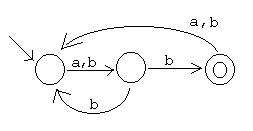
7) Kolik různých jazyků rozhodují automaty s 1/2 stavy nad abecedou {x}/{x,y}?
8) Dokažte, že neexistuje automat se 4 stavy, který akceptuje jazyk:

L={w | w náleží {a,b}^*, |w| >= 4 }
L={w | w náleží {a,b}^*, |w| = 5k , k náleží N₀ } (DÚ)

9) Najděte relaci ~ pod {a,b}^*x{a,b}^*, splňující podmínky Nerodovi věty
a určete její index. Pro jazyk L:

L={w | w náleží {a,b}^*, w obsahuje podslovo abb }

10) Pomocí Nerodovi věty dokažte, že není regulární:

L={aⁿ | n=2ⁱ pro i náleží N₀}
L={aⁿb^m | n <= m <= 2*m ; n,m > 0}
L={ ww^R | w náleží {a,b}⁺ }

11) Pomocí MN věty dokažte, že je regulární:

L={w náleží {a,b}^* | #_a(w) = 3k pro k náleží N₀}

12) Každý jazyk jednoznačně určuje relaci ~_L předpisem
u ~_L v právě když pro každé w platí uw náleží L <=> vw náleží L
Určete index této relace pro jazyky:

L = a^*b^*c^*
L = { aⁿbⁿcⁿ | n >0 }

stav	pod a	pod b
=> 1	2	3
2	5	2
3	3	5
<= 4	12	2
<= 5	7	8
6	4	9
7	12	11
8	4	6
9	10	8
<= 10	3	2
<= 11	12	6
12	3	10