i3dlib

Documentation

i3d::AOSTVFilter

i3d::AOSTVFilter< VOXELIN, VOXELOUT > Class Template Reference
[Image preprocessing filters]

This class implements the Total Variations nonlinear diffusion filter and the Ballanced Forward Backward filter, which were published by Andreu et al. and Keeling et al. As the other nonlinear filters, these filter smooths the image in the relatively continuos region and do not smooth the significante edges. In the typical output image is suppresed the noise and the edges remain sharp and well localised. The diffused image is the solution of the equation 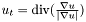$ u_t = \mathrm{div}(\frac{\nabla u}{|\nabla u|}) $. More...

#include <LevelSet.h>

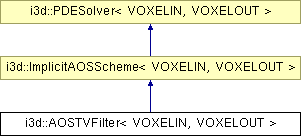
Inheritance diagram for i3d::AOSTVFilter< VOXELIN, VOXELOUT >:

i3d::ImplicitAOSScheme< VOXELIN, VOXELOUT > i3d::PDESolver< VOXELIN, VOXELOUT > List of all members.

Public Member Functions

void SetExponent (VOXELOUT exp)
 Set the Exponent parameter.
VOXELOUT GetExponent ()
 Get the value of the exponent parameter.
void SetBeta (VOXELOUT B)
 Set the Beta parameter.
VOXELOUT GetBeta ()
 get the value of the beta parameter
virtual void ComputeDiffusivity ()
 This function computes the diffusivity g function.

Detailed Description

template<class VOXELIN, class VOXELOUT>
class i3d::AOSTVFilter< VOXELIN, VOXELOUT >

This class implements the Total Variations nonlinear diffusion filter and the Ballanced Forward Backward filter, which were published by Andreu et al. and Keeling et al. As the other nonlinear filters, these filter smooths the image in the relatively continuos region and do not smooth the significante edges. In the typical output image is suppresed the noise and the edges remain sharp and well localised. The diffused image is the solution of the equation 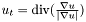$ u_t = \mathrm{div}(\frac{\nabla u}{|\nabla u|}) $.

The well known Total Variation restoration (Rudin et al.) technique tries to to reconstruct the true image u from the observation f. Given an image function 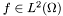$ f \in L^2(\Omega)$, with 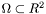$ \Omega \subset R^2$ an open and bounded domain, the problem is to extract u from f. The observation f is usually noised version of u.So Rudin, Osher and Fatemi have proposed following minimization problem:

\[ \inf_u F(u) = \int_{\Omega} |\nabla u| + \lambda \int_{\Omega} |f - u|^2 dx dy \]

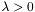where $ \lambda > 0$ is weight parameter, 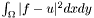$ \int_{\Omega} |f-u|^2 dxdy$ is fidelity term, which holds image u "near" image f, and 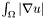$ \int_{\Omega} |\nabla u|$ is the noise removing regularizing term. This minimization problem leads to solving the Euler-Lagrange equation:

\[ u = f + \frac{1}{2 \lambda} \mathrm{div} \left ( \frac{\nabla u } { | \nabla u | } \right ) \]

If we omit the fidelity term, we get in the context of nonlinear diffusion filtering following equation

\[ u_t = \mathrm{div} \left ( \frac{\nabla u } { | \nabla u | } \right ) \]

Some authors add some regularising constant to the equation

\[ u_t = \mathrm{div} \left ( \frac{\nabla u } { (\sqrt { | \nabla u |^2 + \beta })^e } \right ) \]

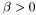,where $ \beta > 0$ is the user selected constant. The exponent e should be greater or equal than 1. For the exponent e=1 we get the Total variation diffusion filter (Andreu et al.) and for exponent e = 2.0 we get the Ballanced Forward Backward filter of Keeling et al.. If we set exponent e between 1 and 2, we get the combination of both filters.

The implementation of this class is based on the articles
Joachim Weickert, Bart M. ter Haar Romeny, Max A. Viergever, Efficient and Reliable Schemes for Nonlinear Diffusion Filtering , IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 6, NO. 3, PP. 398-410, MARCH 1998.
F. Andreu, V. Caselles, J. I. Diaz, J. M. Mazón, Qualitative properties of the total variation flow, Journal of Functional Analysis, Vol. 188, No. 2, 516-547, Febr. 2002.
Stephen L. Keeling and Rudolf Stollberger,Nonlinear anisotropic diffusion filtering for multiscale edge enhancement,Inverse Problems, Vol. 18, 2002, 175--190
L. Rudin, S. Osher, and E. Fatemi, Nonlinear total variation based noise removal algorithms, Physica D, vol. 60, pp. 259-268,1992.

The example code for using the TV diffusion filter. 

   .....
   
   Image3d<GRAY8> i;
   Image3d<float> fimg;
   i.ReadImage('input.tif'); // read input image
   AOSTVFilter<GRAY8,float> TV(i,fimg); // instantiate  the filter  (the two parameters are the input and the output image)
   TV.SetMaximumNumberOfIterations(3); // Set the number of iterations to 2
   TV.SetSpacing(1.0,1.0,2.0); // Set the spacing of spatial discretisation to 1,1,2
   TV.SetGlobalTimeStep(5.0); // Set the global time step
   TV.Execute(); // Perform the work of the filter
   FloatToGray8NoWeight(fimg,i); //Convert the output float image to gray8 image
   i.SaveImage('output.tif'); // save the output of the filter

   ......
Author:
Jan Hubený xhubeny@fi.muni.cz
Date:
2005

The documentation for this class was generated from the following files:

Generated by doxygen