10. Rekurze¶
Syn: Kolik otoček potřebuji na zašroubování žárovky?
Otec: Pokud už je zašroubovaná, tak 0.
Jinak ji zatoč jednou, zeptej se mě znova a k mé odpovědi přičti 1.
Rekurze je využití sebe sama. Typickými příkladem je rekurzivní definice, tedy použití X v definici X. Můžeme třeba definovat funkci faktoriál pomocí funkce faktoriál:
0! = 1
n! = n * (n - 1)! pro n > 0
Totéž ve slovech:
Syn: Kolik je faktoriál čísla n?
Otec: Pokud je n rovno 0, pak 1.
Jinak se mě zeptej na faktoriál čísla (n - 1) a moji odpověď vynásob číslem n.
Při programování se pak rekurze objeví jako funkce, která pro výpočet
využívá sebe sama. Téměř jedna ku jedné můžeme k definici matematické
funkce faktoriál napsat definici výpočetní funkce faktorial v Pythonu:
(faktorial_demo)
Nejedná se o definici v kruhu, protože v každém kroku dochází ke zjednodušování (faktoriál n je definován pomocí faktoriálu n - 1) a je definován i bázový případ (n = 0) bez rekurze, ke kterému vše směřuje. Jde tedy spíše o definici ve spirále.
Jak postupovat při návrhu rekurzivních algoritmů? Nejprve určete
podproblémy, které potřebujete k vyřešení vašeho problému (například pro
výpočet n! potřebuji určit jediný podproblém (n - 1)!) Tyto
podproblémy vyřešte rekurzivně a z jejich výsledků poskládejte výsledné
řešení. Dále je nutné určit bázový případ (případně více bázových případů)
a jejich řešení (například faktoriál 0 je 1). Bázový případ musí být
takový, aby se k němu všechny větve výpočtu časem dostaly, jinak by výpočet
nikdy neskončil.
Další ukázkou rekurzivního algoritmu je výpočet největšího společného dělitele, zde už však není 1 ku 1 korespondence s obvyklou definicí největšího společného dělitele. Korektnost funkce tady vyplývá z korektnosti zjednodušovacího rekurzivního kroku (\(nsd(a, b) = nsd(a \mod b, b)\) pro b > 0) a bázového případu (\(nsd(a, 0) = a\)), ke kterému výpočet nevyhnutelně směřuje (a v konečném počtu kroků se k němu dostane).
(nsd_demo)
10.1. Zmenši a panuj¶
Mnoho problémů lze řešit tak, že nejprve vyřešíme zjednodušenou verzi problému a řešení zjednodušeného problému rozšíříme na řešení původního problému. Nejčastější variantou je redukce na problém s o 1 menším vstupem (viz faktoriál výše), někdy je však možné zmenšit velikost vstupu na polovinu a zmenšování může být dokonce i nepravidelné (jako v případě Euklidova algoritmu pro NSD výše). Této technice se říká zmenši a panuj, anglicky decrease-and-conquer. Může být implementována buď iterativně (pomocí cyklu) nebo rekurzivně (funkce s jediným rekurzivním voláním).
10.1.1. Součet čísel¶
Napište rekurzivní funkci, která zjistí součet přirozených čísel od 1 do
n. Při vymýšlení funkce series_sum(n) si představte, že máte k
dispozici funkci series_sum(k) pro libovolné k < n. Nezapomeňte na bázový
případ.
def series_sum(n: int) -> int:
pass
def test_series_sum() -> None:
assert series_sum(1) == 1
assert series_sum(5) == 15
assert series_sum(10) == 55
assert series_sum(100) == 5050
10.1.2. Prvek posloupnosti¶
Napište rekurzivní funkci, která počítá n-tý prvek posloupnosti definované následujícím induktivním způsobem:
\(a_0 = 5\)
\(a_n = 2 \cdot a_{n - 1} - 1\)
def sequence(n: int) -> int:
pass
assert sequence(0) == 5
assert sequence(1) == 9
assert sequence(2) == 17
assert sequence(3) == 33
10.1.3. Zašroubování žárovky¶
Napište rekurzivní funkci, která n-krát vypíše „twist“.
def screwing(n: int) -> None:
pass
screwing(3)
# Ocekavany vystup:
# twist
# twist
# twist
10.1.4. Součet seznamu čísel¶
Napište rekurzivní funkci pro součet seznamu čísel.
def list_sum(numbers: List[int]) -> int:
pass
def test_list_sum() -> None:
assert list_sum([1, 8, 2, 0, 4, 2]) == 17
10.1.5. Binární vyhledávání¶
Napište funkci binary_search(value, numbers), která zjistí, zda se hodnota
value nachází ve vzestupně uspořádaném seznamu numbers. Funkce musí
mít logaritmickou časovou složitost. Pozor na to, že kopírování seznamu má
lineární časovou složitost vzhledem k počtu prvků. Je tedy vhodné napsat si
pomocnou funkci, která bude hledat zadané číslo v části seznamu ohraničeném 2
parametry (např. left a right pro levou a pravou mez intervalu, ve
kterém hledáme).
def binary_search(value: int, numbers: List[int]) -> bool:
pass
def test_binary_search() -> None:
assert binary_search(5, [1, 2, 5, 8]) == True
assert binary_search(4, [1, 2, 5, 8]) == False
10.2. Rozděl a panuj¶
Někdy je potřeba k vyřešení problému nejprve vyřešit hned několik podproblémů a potom zkombinovat řešení podproblému do výsledného řešení. Této technice návrhu algoritmů se říká rozděl a panuj, anglicky divide-and-conquer. Zatímco v předchozí sekci byla složitost napsání iterativní a rekurzivní implementace téměř stejná, u algoritmů navržených touto technikou bývá rekurzivní implementace výrazně jednodušší a elegantnější. (Odstranit rekurzi je ale vždy možné pomocí zásobníku.)
10.2.1. Hanojské věže¶
Máme 3 věže, na jedné z nich (budeme jí říkat zdrojová), je nasunuto n kotoučů různé velikosti od největšího po nejmenší. Úkolem je přesunout všechny kotouče ze zdrojové na cílovou věž, přičemž vždy můžeme přesouvat pouze jeden kotouč a nikdy nesmíme dát větší kotouč na menší. Pokud jste se s hrou ještě nesetkali, vyzkoušejte si ji. Naším úkolem teď bude vymyslet rekurzivní algoritmus, který přesune n kotoučů ze zdrojové na cílovou věž, resp. vypíše kroky, které je potřeba k přesunu udělat. Řešení pro 3 kotouče, a věže pojmenované ‘A’ (zdrojová věž), ‘C’ (cílová věž) a ‘B’ (pomocná věž):
>>> hanoi(3, 'A', 'C', 'B')
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
# Vypise premistovani kotoucu pri reseni Hanojskych vezi.
# - n: pocet kotoucu
# - source: tyc, na ktere jsou kotouce na zacatku
# - target: tyc, na kterou chceme kotouce premistit
# - auxiliary: pomocna tyc, kterou lze vyuzit v prubehu premistovani
def hanoi(n: int, source: str, target: str, auxiliary: str) -> None:
pass
hanoi(3, 'A', 'C', 'B')
10.2.2. Hanojské věže graficky¶
Rozšiřte předchozí úlohu o vykreslování mezistavů po každém přesunu pomocí ascii grafiky.
>>> hanoi(3, 'A', 'C', 'B')
# | |
### | |
##### | |
----- ----- -----
A B C
| | |
### | |
##### | #
----- ----- -----
A B C
...
10.2.3. Maximum a minimum¶
S využitím techniky rozděl a panuj napište funkci pro zjištění minima a maxima ze seznamu čísel. Vaše funkce by měla obsahovat 2 rekurzivní volání. Zkuste se vyhnout kopírování části seznamu (podobně jako v úloze Binární vyhledávání).
def min_max(numbers: List[int]) -> Tuple[int, int]:
pass
def test_min_max() -> None:
assert min_max([8, 4, 3, 5, 9, 2, 1, 7, 6]) == (1, 9)
10.2.4. Rychlé řazení¶
Metodu rozděl a panuj lze využít k efektivním algoritmům pro řazení. Jeden z možných přístupů je vybrat libovolný prvek (tzv. pivot), a všechna ostatní čísla rozdělit na 2 části – menší než pivot a větší než pivot. Tyto dvě části seřadíme rekurzivně a spojíme do výsledného pole. Rozdělení čísel na prvky menší a větší než pivot je jednoduché, pokud povolíme vytvářet nové seznamy (tím se mírně zhoršuje paměťová složitost). Implementujte tento rekurzivní algoritmus, nezapomeňte na bázový případ. Můžete si přečíst podrobnosti o QuickSortu na Khan Academy a pokusit se implementovat rozdělování prvků na místě (bez potřeby vytváření nových seznamů).
# vraci serazene pole 'array' (samotne pole 'array' nemeni)
def quick_sort(array: List[int]) -> List[int]:
pass
def test_quick_sort() -> None:
assert quick_sort([2, 7, 8, 1, 4, 5, 9, 3, 6]) == list(range(1, 10))
10.3. Fraktály¶
Rekurze je příkladem obecnějšího jevu odkazování na sebe sama, tzv. sebe-reference. Sebe-reference se vyskytuje v jazyce (Třeba tato věta mluví sama o sobě.), v knihách, v divadle, ve filmu, ale dokonce i v matematice. Sebe-reference je dokonce hlavní ingrediencí nejslavnějších důkazů matematiky (Gödelovy věty o neúplnosti) a také informatiky (existence problémů, pro které neexistuje algoritmus, který by je řešil – např. problém zastavení).
Vedle rekurze jsou nejtypičtějším zástupcem sebe-reference fraktály, obrázky, které jsou soběpodobné, tedy jejich části připomínají obrázek jako celek. Fraktály můžete objevit všude možně v přírodě (např. větve stromů, kapradina). Fraktály a rekurze nejsou dva nezávislí reprezentanti sebe-reference, i mezi nimi je silná souvislost. Rekurze je totiž velmi elegantní způsob, jak jednotlivé fraktály definovat. Díky tomu často můžeme složité fraktály vykreslit pomocí jednoduchých rekurzivních funkcí.
Technická poznámka:
Ke kreslení fraktálů využijeme knihovnu turtle, se kterou jsme
pracovali v první kapitole. Nezapomeňte po dokončení kreslení zavolat
funkci done z této knihovny (měl by to být poslední řádek vašeho
programu, rozhodně ji nevkládejte do rekurzivní funkce, jinak bude kreslení
ukončeno předčasně).
10.3.1. Vnořené čtverce¶
Úkolem je napsat rekurzivní funkci, která vykreslí vnořené čtverce. Parametr funkce bude udávat, kolik čtverců má být vykresleno. Při vymýšlení rekurzivní funkce si nejprve ujasněte (můžete zapsat do komentáře), co funkce dělá – není důležité jen to, co želva vykreslí, ale také to, kde skončí a jakým směrem bude natočená. Dále si představte, že již máte k dispozici funkci, která umí kreslit menší počty čtverců a využijte ji k napsání těla funkce. Nezapomeňte na bázový případ. Funkce bude obsahovat jediné rekurzivní volání, takže by bylo jednoduché ji přepsat pomocí cyklu bez rekurze (můžete si vyzkoušet).
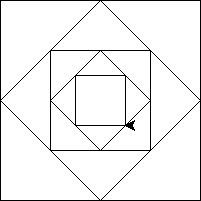
from turtle import Turtle
julie = Turtle()
julie.speed(10)
# depth: kolik ctvercu vykreslit
# length: delka strany nejvetsiho ctverce
def nested_squares(depth: int, length: float = 180.0) -> None:
pass
nested_squares(8)
10.3.2. Strom¶
S využitím techniky rozděl a panuj napište rekurzivní funkci pro vykreslení stromku, jako vidíte na obrázku. Po vykreslení základního stromku můžete vyzkoušet různé variace, např. změnit stupeň větvení, délku větví, naklonění větví atd.
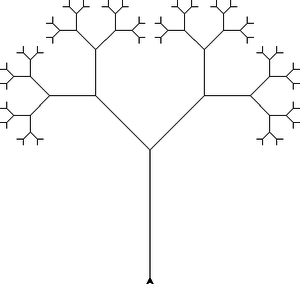
from turtle import Turtle
julie = Turtle()
julie.speed(10)
julie.left(90)
# length: delka kmenove cary
def tree(length: float) -> None:
pass
tree(90)
10.3.3. Kochova vločka¶
Napište rekurzivní funkci pro vykreslení Kochovy křivky. Vhodným složením tří Kochových křivek (jakoby do trojúhelníka) získáte Kochovu vločku.
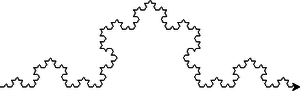
from turtle import Turtle
julie = Turtle()
julie.speed(10)
julie.setposition(-190, 0)
# depth: pocet rekurzivnich zanoreni
# size: sirka krivky
def koch(depth: int = 5, size: float = 380.0) -> None:
pass
koch(5)
10.3.4. Sierpinského trojúhelník¶
Napište rekurzivní funkci pro vykreslení Sierpinského trojúhelníka (není nutné „nezpracované“ trojúhelníky vyplňovat černou barvou).
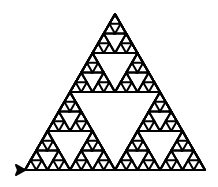
from turtle import Turtle
julie = Turtle()
julie.speed(10)
# depth: pozadovana hloubka rekurzivniho zanoreni
# length: delka strany trojuhelnika
def sierpinski_triangle(depth: int, length: float = 180.0) -> None:
pass
sierpinski_triangle(5)
10.3.5. Fraktálové sušenky¶
Fraktály mají své místo i v kuchyni. Příkladem mohou být fraktálové sušenky, připomínající Sierpinského koberec. I tento fraktál lze poměrně snadno vykreslit pomocí želví grafiky. Pro vyplňování čtverců barvou můžete použít funkci fill z knihovny turtle.
Pokud byste si chtěli fraktálové sušenky upéct, přikládáme mnoholetou praxí ověřený recept (nezapomeňte donést ochutnávku na cvičení). Stejně jako kreslení fraktálů, i jejich pečení je výhodné provádět rekurzivně, není tedy překvapením, že zmíněný recept je rekurzivní. Můžete také vymyslet jiné sebe-referenční pochoutky.


from turtle import Turtle
julie = Turtle()
julie.speed(10)
julie.setposition(-180, -180)
# vykresli ctverec bez vyplne
def empty_square(length: float) -> None:
for i in range(4):
julie.forward(length)
julie.left(90)
# vykresli vyplneny ctverec
def filled_square(length: float) -> None:
julie.pendown()
julie.begin_fill()
for i in range(4):
julie.forward(length)
julie.left(90)
julie.end_fill()
# funkce pro vykresleni Sierpisnkeho koebrce
# depth: pozadovane rekurzivni zanoreni
# length: delka strany
def sierpinski_carpet(depth: int, length: float = 360.0) -> None:
# nechceme, aby pri presunech zelva kreslila
julie.penup()
# ---------------------------------------
# TODO: dopiste tuto rekurzivni funkci
# ---------------------------------------
# vykresli fraktalovou susenku
def fractal_cookie(depth: int, length: float = 360.0) -> None:
# okraj
empty_square(length)
# vnitrek
sierpinski_carpet(depth, length)
fractal_cookie(3)
10.3.6. Hilbertova křivka¶
Napište funkci pro vykreslení Hilberotvy křivky.

from turtle import Turtle
julie = Turtle()
julie.speed(10)
def hilbert(depth: int = 4, right: bool = True, length: int = 10) -> None:
pass
hilbert()
10.4. Akumulátor¶
Při psaný funkcí s více rekurzivními voláními je potřeba dávat pozor na to, jestli se výpočty jednotlivých volání nepřekrývají. Klasickým odstrašujícím příkladem je výpočet n-tého Fibonacciho čísla. Následující naivní rekurzivní algoritmus vede k exponenciální časové složitosti.
def fibonacci_disaster(n: int) -> None:
if n < 2:
# bazove pripady
return n
else:
# rekurzivni volani
return fibonacci_disaster(n - 1) + fibonacci_disaster(n - 2)
print(fibonacci_disaster(30))
To však neznamená, že nelze Fibonacci čísla počítat pomocí rekurze
efektivně, je však potřeba zvolit jiný přístup. Lze použít techniku
akumulátoru, díky níž nám postačí jediné rekurzivní volání na konci funkce
(tzv. koncová rekurze, anglicky tail recursion). Myšlenka je stejná jako
u iterativního výpočtu Fibonacciho čísel cyklem – udržujeme si poslední 2
vypočítaná Fibonacciho čísla a kolik čísel nám ještě zbývá napočítat, než
se dostaneme k požadovaném Fibonaccimu číslu. Časová složitost je pak
lineární vzhledem k n.
(fibonacci_acc_demo)
10.4.1. Tetranacciho posloupnost¶
Napište efektivní rekurzivní funkci pro výpočet n-tého čísla Tetranacciho posloupnosti, která je definovaná následujícím induktivním způsobem:
\(a_0 = 0\), \(a_1 = 1\), \(a_2 = 1\), \(a_3 = 2\),
\(a_n = a_{n - 1} + a_{n - 2} + a_{n - 3} + a_{n - 4}\)
10.5. Doplňující zdroje¶
Robotanik (umimeprogramovat.cz) (Skvělé na procvičení rekurzivního uvažování.)