How To Distribute LTL Model-Checking Using Decomposition of Negative Claim Automaton

How To Distribute LTL Model-Checking Using Decomposition of Negative Claim Automaton |
 |
Jiri Barnat | |
| barnat@fi.muni.cz |
Abstract:
We propose a distributed algorithm for model-checking LTL formulas that
works on a network of workstations and effectively uses the decomposition
of the formula automaton to strongly connected components to achieve more
efficient distribution of the verification problem. In particular, we
explore the possibility of performing a distributed nested depth-first
search algorithm.
LTL Model-Checking:
Model-Checking is
a problem of decision whether a model of a given system satisfies a simple
property expressed as a formula of some temporal logic. In the case of
Linear Temporal Logic (LTL) the model-checking problem can be reduced
to the problem of emptiness of Buchi automata.
To solve the problem
so called Product Automaton is built. The product automaton is a
result of a synchronization of the small Negative Claim Automaton
with a huge System Automaton (with all states considered as
accepting). The system automaton models the behavior of the given system and
the Negative Claim Automaton describes the behavior which contradicts the verified property. If
the language of the product automaton is not empty then the system has some
illegal behavior which means that verified property is not satisfied.
Sequential Algorithmic Solution: The standard algorithm used to solve the problem is the Nested Depth-First Search algorithm.
PROCEDURE DFS(state)
IF (state,0) not in visited_set
THEN visited_set := visited_set + (state,0)
in_stack_set := in_stack_set + state
FOREACH s in Succ(state) DO
DFS(s)
IF Accepting(state)
THEN NDFS(state)
FI
in_stack_set := in_stack_set - state
FI
END
PROCEDURE NDFS(state)
IF (state,1) not in visited_set
THEN visited_set := visited_set + (state,1)
FOREACH s in Succ(state) DO
IF s in in_stack_set
THEN Report("Cycle")
ELSE NDFS(s)
FI
FI
END
Since the algorithm has to maintain all already explored states the
algorithmic solution suffers from the space requirements (well known state
explosion problem).
Distributed Algorithmic Solution
A possible
way how to deal with the state explosion problem is the utilization of
computation power of several interconnected workstations (network nodes).
Unfortunately, performing the Nested DFS algorithm on several processors in
parallel may result in an incorrect behavior of the algorithm. In that case
the algorithm may not discover existing accepting cycle.
We can assure the correctness of the distributed Nested DFS algorithm by
defining such a partition of the state space in the distributed environment
that preserves locality of cycles in the Product Automaton graph and by
limiting the nested part of the algorithm to those successors of a state
that are local on the network node.
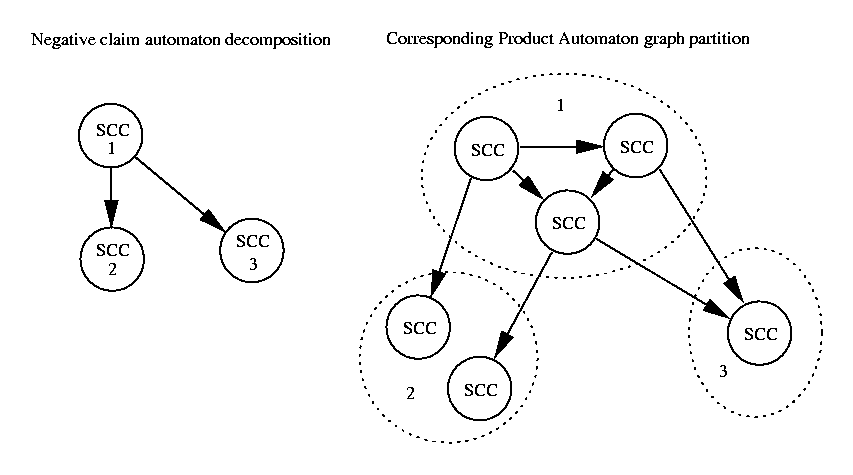
The key observation for an implementation is that the states of Product
automaton are pairs. Each pair is made by a state of the system automaton
and by a state of the Negative Claim Automaton. Hence, whenever there is a cycle C in the product
automaton then there is a corresponding cycle D in the Negative Claim Automaton.
Experimental Results
| Modeled system: | Elevator II |
| Verified property formula: | G(r0 -> (!p0 U (p0 U (!p0 U (p0 && o))))) && | G(r1 -> (!p1 U (p1 U (!p1 U (p1 && o))))) |
| The number of SCCs in Negative Claim Automaton decomposition: | 11 |
| Sequential NDFS | Distributed NDFS (11 nodes) | |
| Visited states | 542324 | maximum per node = 119773 (22%) |
| Running time (seconds) | 28.35 | 19.29 |
Conclusion
The main novelty of proposed algorithm is that we use the decomposition of
the Negative Claim Automaton into maximal strongly connected components to
distribute the verification problem over the network. In addition to the
fact that we are able to decompose the task several instances of the
verification procedure can be performed in parallel. This approach to the
distribution of the algorithm can be used in the framework of multi-thread
programming as well. We would like to point out that the technique is
independent of the others distribution techniques, hence, it can be
fruitfully combined with them.